RESEARCH

RESEARCH LINES

1. Mechanisms of plastic deformation of ceramic polycrystals at high temperature

          Advanced ceramics have been preferential systems for scientists and engineers throughout the 20th century. This interest has been greatly based upon the particular physical properties exhibited by some of these systems, which make them optimum for certain functional applications; for instance, UO2 is used in nuclear reactors, ZrO2 is a component of fuel cells and some YBaCuO are superconductors. Some other ceramics are interesting due to their potential structural applications; for instance, the superplasticity of ZrO2 (similar to that of the metals) was discovered in 1986. Anyway, the study of the mechanical behavior of ceramics is relevant; in the case of functional materials, because their integrity must be guaranteed under working conditions. In structural ones, the mechanical properties are inherently interesting.                 

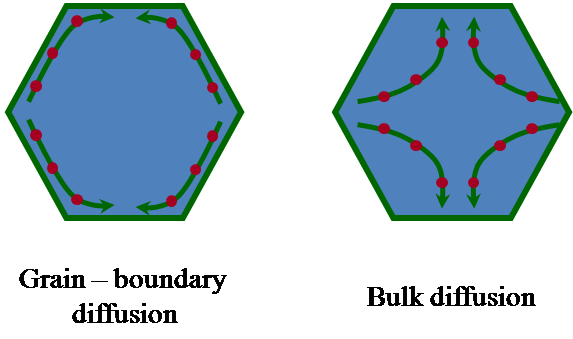          In general terms, creep denotes the process of plastic deformation of a material at temperatures above 0.5Tm, where Tm is the melting temperature of the material, under the action of an external, an generally uniaxial, stress. The relevant physical properties in a creep process are the strain rate, the strain to failure and the creep stress, among others. In polycrystals, the plastic deformation proceeds either by diffusion or by grain boundary sliding; the latter does not involve any change in the grain shapes. In all cases, internal stresses are generated at the grains during the plastic deformation, which must be released in order to avoid the eventual failure of the material. The process by which the internal stresses are relaxed is called accommodation mechanism, and uses to be diffusional in nature. The various mechanisms differ to each other by the process responsible of the deformation (diffusion or grain boundary sliding) and by the accommodation process (which determines the strain rate at which the material creeps).

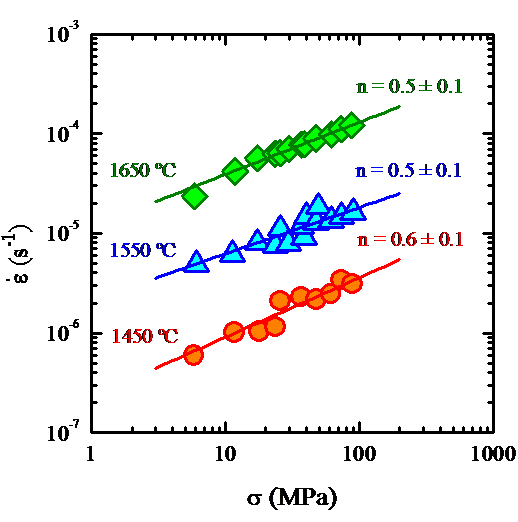
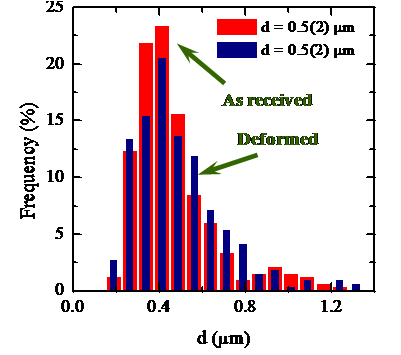          The identification of the deformation mechanisms in polycrystals takes place by a sequence of mechanical tests, which allow characterize the process macroscopically, and microstructural observations of the samples before and after the deformation. The comparison of both microstructures allows one obtain information about the primary and accommodation processes and thence to identify the deformation mechanism. Since 1998 I have been studying the plastic deformation at high temperatures of ceramic materials in collaboration with the University of Sevilla. These ceramics have been either oxidic (SiC whiskers-reinforced alumina [1, 4], aluminum titanate stabilized with oxides and doped with mullite [2], zircon [3] and mullite [10]) and, mainly, non-oxidic (like ZrB2 [8], SiC [21] and, above all, Si3N4 [7, 13, 14]). Among these works, the study of two gas-pressure sintered silicon nitride ceramics containing a secondary glassy phase is outstanding. The high temperature mechanical tests (performed at temperatures between 1450 ºC and 1750 ºC) yielded a stress exponent systematically lower than one (with an average value of about 0.5) for both samples under all the experimental conditions. The microstructural observations were consistent, in principle, with a grain boundary mechanism accommodated by solution-precipitation. However, the results were surprising because all the commonly invoked models for creep in this type of materials predicts stress exponents equal to 1 or between 1 and 2.

          For instance, this is so in the Wakai "step" model for solution - precipitation. Essentially, it is assumed that the relaxation of the stresses generated during grain boundary sliding takes place by a sequential process consisting in solution of crystalline material in the secondary glassy phase followed by diffusion along this phase and finally precipitation at stress-free grain boundaries. The slowest of these mechanism is the rate-controlling one. Thus, if the lowest one is transport along the secondary phase, the mechanism is said to be diffusion-controlled, and is characterized by a stress exponent n = 1. On the contrary, if the slowest processes are those of solution or precipitation, the mechanism is said to be interface reaction - controlled, and is consistent with stress exponent n = 1 or n = 2. The traditional mechanism of solucion-precipitation is not consistent with stress exponent lower than one in any case.

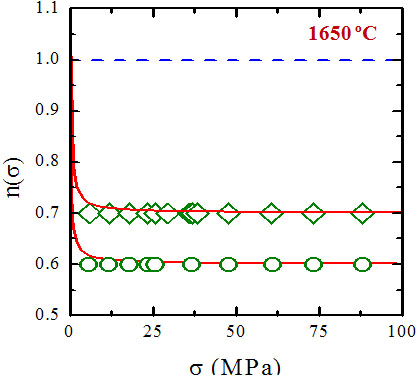          In the original "step" model, Wakai assumes that the solute chemical potential within the grain is identically equal to the one in the supersaturation conditions which give rise to the solution. Using this fact, Wakai calculates a stress exponent which is a function of the applied stress and the temperature; in addition, the numerical values of this exponent are not only greater than one, but also than one hundred in the typical stress and temperature ranges for silicon nitride. This actually constitutes a physical inconsistency of the model. The solution to this inconsistency was to consider in greater detail the solution-precipitation process [12]. In particular, there are two terms which were not included by Wakai in his original calculation; the first of them corresponds to the free energy increment due to the different solute volumes in solution and in solid phase. The second term is associated to the change in the solute chemical potential within the grain and supersaturated at the step under stress. If these two terms (particularly the second) are included, the stress exponent not only acquires the right order of magnitude, but also can be naturally lower than one under certain conditions. Reference [12] thus contains the final form of the solution-precipitation model.

2. Resolution of crystalline structures by X-ray powder diffractometry

          The development the Organic and Inorganic Chemistries nowadays gives rise to the synthesis of a great number of artificial substances. The interest of these compounds lies on their multiple applications: as pigments, catalyzers, agents with luminescent activity and, above all, on their potential biological activity (antitumoral, analgesic, antibiotic, etc.). That is the reason why it is important to know the crystalline structure of some of them.

          In this context, an essential difficulty arises due to that, in general, one does not have single crystals with appropriate size and quality; instead, a good number of the artificial substances are obtained directly as a powder. This fact makes the conventional techniques of structural resolution from X-ray diffractometry not to be valid, so that new resolution strategies must be designed and optimized from powder diffraction diagrams. These correspond to 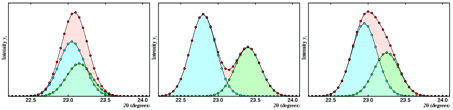two-dimensional representations of the diffracted intensity as a function of the diffraction angle; since, in these cases, the Bragg angle can be the same for different families of planes, the powder diffraction diagrams are characterized because their maxima are generally strongly overlapped. Actually, the difficulty associated to the univocal separation of the different reflections merging at the same maxima is one of the main limitations of the powder diffractometry.

          Formally, the structural resolution of a crystal consists on determine the relative positions of each atom in the asymmetric unit within the unit cell. It is a mathematical problem which can be solved if the structure factors corresponding to a number of hkl directions of the reciprocal space; these structural factors are complex quantities whose phases contain the information about the atomic positions. However, in a diffraction experiment one just gets information about the diffracted intensity for each reflection, which is proportional to the square of the corresponding structure factor; alternatively, one has information about the modulus of the structure factors, but neither about their phase and, therefore, nor in principle about the atomic positions. This fact is the well known "phase problem", where the main difficulty of the structural resolution lies.

          The phase problem is generally solved applying any of the reciprocal space methods, such as the direct methods, whose philosophy essentially consists of recognize that, somehow, the information about the phases is diluted in the set of observed structure factors moduli. Depending on the structure, a number of phases can be arbitrarily assigned, and all the others are obtained by the triplet rule. Direct methods allow solve the structure of a crystal provided that one has at least ten reflections (that is, distinguishable non-overlapped maxima) for each atom in the asymmetric unit. When such a requirement is not fulfilled (for instance, because the molecule is complex, because the experimental data are not good enough, or because de particular conditions make impossible the deconvolution of the peaks) the so-called real space methods must be used. In this case no phases are assigned to the structure factors (and thence the phase problem is not directly solved). Instead, the starting point is the knowledge of the connectivity of the isolated molecular (which is generally known from spectroscopy), and the structural resolution proceed by a Monte Carlo algorithm oriented to the minimization of a certain cost function. Finally, the various interesting parameters are refined by the Rietveld method to reach a reasonable degree of precision [15].

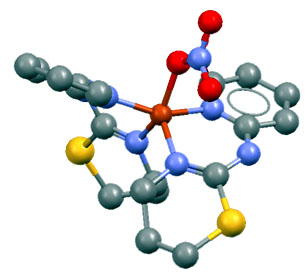
          This resolution strategy has been successfully applied to the structural determination of different substances of biological interest in collaboration with the Synthesis Group of the Department of Inorganic Chemistry of the University of Extremadura. This group works mainly on the synthesis of coordination complexes (which, essentially, are formed by joining a metallic cation to an organic or organometallic anion called ligand), so that the main structures resolved belonged to these. The first one was the complex [Cu(NO)3-(PITz)2]NO3 (with PITz = 2-(2-pyridil)iminotetrahidro-1,3-thiazine) [15]; the second was the complex ZnCl2(TdTz) (with TdTz = 2-(3,4-dichlorephenil)imino-N-(2-thiazin-2-il)thiazolidine) [17]. The analysis of the bond distances and angles and torsion angles fulfilled all the chemical requirements, so that both solutions were considered satisfactory, and were successfully deposited in the CCD (Cambridge Crystallography Database) database.

          Recently, a new ab initio method for structural resolution has received considerable attention. The nucleus of this method consists of a relatively simple algorithm –the charge flipping algorithm. This algorithm is a cyclic process, each cycle containing four stages. Initially, random phases are assigned to the structure factor amplitudes derived from the observed intensities, which allows plot a (random) charge density map ρ(r). In the first stage, the signs of all the electron densities in the map below a certain threshold value δ (being δ a small positive number) are reversed, which results in a modified electron density map g(r). In the second stage, a fast Fourier transform (FFT) allows a set {G(q)} of temporary structure factors to be generated. In the third stage, the phases of these G’s are combined with the moduli of the original structure factors, which gives rise to a second set {H(q)} of structure factors, whose phases are no longer random. Finally, the inverse FFT allows plot a new charge density map, which is used as starting point for the second cycle. The iterative process goes on until convergence is reached. The charge flipping method can solve the structure in the space group P1, so that no previous knowledge about symmetry is required. Information about either the chemical composition or the type of atoms presents is not needed either, so that the procedure is indeed ab initio. The method has been successfully applied in two relatively complex situations. In the first one, it was used to solve the structure of [NBu4]2[Pd2{C4(COOMe)4}2(µ-OH)2], characterized by having a relatively high number of atoms (156 non hydrogen ones) in its asymmetric unit [29]. In the second one, the algorithm was used to solve the structure of ZnCl2(BzTz)2 [with BzTz = N-(5,6-dihydro-4H-1,3-thiazin-2-yl)-2-aminobenzimidazole], which is characterized by exhibiting continuous positional disorder in some of its atoms [30].

3. Mechanical properties of materials at intermediate temperatures

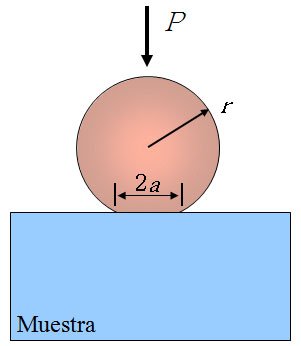          Ceramic materials are brittle, so that at temperatures below the creep ones do not exhibit plasticity. The magnitudes of interest are different to the relevant at high temperatures. For instance, at room temperature, the study of these systems consists of performing alternative mechanical tests, like those of indentation, which allow determine magnitudes such as elastic modulus, hardness, toughness or fracture strength. Among these tests, the indentation with spheres (or Hertz indentations) are particularly important because the contact is initially elastic. By means of this type of tests one can get the indentation stress - strain curve and, from it, information about the mechanical properties of a material.

          Part of our research has been useful to develop a new methodology to extend the used at room temperature to temperatures close to creep ones [22]. To that end, a high-temperature furnace was coupled to the Hertz indentation device (built with the proper refractory material, namely alumina or silicon nitride) to obtain the indentation stress-strain curve at a given temperature. The elastic modulus of the material at that temperature was trivially calculated from the lineal part of the curve. Subsequently, the stress-strain curve is modeled as the superposition of two regions, one corresponding to a purely elastic contact and the other to a plastic deformation with a given work hardening parameter; the adjustable parameters are thus the yield stress (Y) and the work hardening parameter (n). Using the finite element method (FEM) these parameters are fitted by trial and error until obtaining a simulated stress-strain curve which overlaps with the experimental one; when it happens, the calculated Y and n parameters are those of the material at the given temperature. This method has been successfully applied to the mechanical behavior at intermediate temperatures of polycrystalline Al2O3 [25] and ZrO2 [27].

          In addition to these studies, within this research line I have collaborated in the study of the fatigue of silicon single crystals [26]. Due to the highly covalent nature of its bonding, silicon has traditionally been regarded as a material immune to slow crack growth (SCG) and, therefore, to mechanical fatigue. Let us consider then that silicon is submitted to Hertz indentation tests under some indentation load (well below the failure load but higher than the critical load for initiation of cone cracks) kept for different time intervals. One of the ways to measure the strength of silicon under these conditions consists of fixing it to a transparent and soft substrate (for instance, a polycarbonate), with the damage in contact with the substrate, and to apply a increasing load with a sphere until some damage is observed. Normally, this is a radial crack which finally causes failure. The load under which the radial crack reaches the silicon - polycarbonate interface allows calculate the fracture strength of silicon. If silicon is immune to SCG, then its strength should be the same regardless the time of application of the indentation load; this is indeed which one observes experimentally.

          Now, if the applied indentation load is not static, but cyclic (that is, if the peak load is applied at a given frequency), then a sharp decrease in the strength is observed at a critical number of cycles, which demonstrates that silicon exhibits fatigue under these conditions. This same effect has been observed under different indentation loads. The implications in the behavior of microelectromecanic and nanoelectromecanic systems are evident. The original work [26] constituted the first experimental evidence of fatigue in silicon single crystals. In addition, it was possible to identify the fatigue mechanism [28], which shows three clear stages:

• The first one corresponds to the first few cycles, and is associated to the surface damage induced by the contact. According to the results obtained in tests performed in micromachined samples, this first stage causes defects of about 1 micron in size.
• The second step corresponds to the extensive degradation of the silicon surfaces once the first cone crack has appeared. The dynamical process on the created cracks causes ejection of material from the crack walls and the proliferation of more cracks, which suggests the existence of a marked friction between the crack surfaces which accelerates the surface damage process.
• Finally, a third stage may be identified, which is associated to the smearing and crushing of ejected particles and debris at ring crack segments closer to the contact circle. When the ejected particles enter into contact with the indenter they are compressed and expanded, which makes them to act themselves as indenters which erode the solid external surface finally causing catastrophic failure.

4. Numerical simulation of solids at atomic scale

          During last years, simulation techniques at atomistic scale (particularly Molecular Dynamics and its variants) have been successfully applied due to the hardware and algorithm development. The success of these lies essentially on its low cost, in the possibility to accurately control microscopic parameters and to achieve experimental conditions hard to find in conventional laboratories. In particular, my interest focuses on the study of the structure and dynamics of the grain boundaries in a polycrystal. This study is a fundamental aspect in the development of advanced materials due to the effect that these boundaries have in their macroscopic behavior. The grain boundaries are structural defects of relatively high energy which constitute preferential regions for the localization of other defects affecting the physical properties; in addition, the movement of the grain boundaries controls kinetics during the processing of polycrystals, and therefore determines morphological parameters such as grain size or texture, on which those properties depend. Anyway, the knowledge of the dynamics of grain boundaries at atomistic scale is a first step when one tries to develop a multiscale model for plasticity in polycrystals.

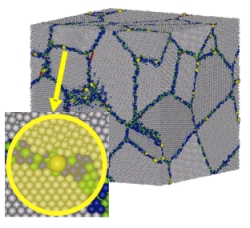          The dynamics of grain boundaries is extremely sensitive to the presence of impurities. This fact is crucial in doped polycrystals, where, under some conditions, the solute atoms tend to segregate to the grain boundaries to reduce the energy of lattice deformation; the importance of segregation lies on that it couples to the dynamics of grain boundaries. There have been developed several theoretical models for the impurities segregation in grain boundaries, which have either an thermodynamical/statistical nature or use a space-charge point of view. Generally, these works provide with quantitative information about segregation, although they neglect the atomistic structure of the grain boundaries and the interactions between constituents at that scale, which is a handicap. In addition, most of the mentioned models deal with equilibrium conditions, quite fa away from the real situation in working conditions. There are also models for dynamics of grain boundaries in presence of impurities.

          The challenge consists then of studying the dynamics of grain boundaries and its coupling to impurities segregation under non-equilibrium conditions by numerical simulation. A number of the works on simulation of dynamics of grain boundaries has been devoted to the study of their mobility as a function of the microstructural parameters or the external variables. By means of Molecular Dynamics (MD) it has been possible to show then that grain boundary migration and sliding occur simultaneously and, if the geometrical constraints imposed by the triple points of the grain structure are not severe, both give rise to rotation of the grains themselves. MD has also been successfully used to study Coble creep and the role played in it by grain boundary sliding and migration. Finally, it is also noteworthy that MD has allowed study the correlation between grain boundary sliding, diffusional creep and normal grain growth.

          Despite the advance associated to the use of simulation techniques, there are many open problems, some of which are crucial. In most of the works, impurities are randomly distributed, and their evolution takes place either by pure diffusion or due to the action of a driving force which causes the movement of the grains. In no case the characteristics of the impurities diffusion or the interactions between them are studied. Regarding the movement of the grain boundaries, it is commonly regarded that they evolve under the action of temperature; the effect of external stresses has not been systematically studied. In addition, it is generally accepted that the movement of the grain boundaries is induced by a driving force which is proportional to the grain curvature. However, when aliovalent impurities are present, a local electric field at the grain boundaries exists, which affects diffusivity. The existence of this field has an important effect on the dynamics of grain boundaries, which causes, among others, the apparition of a threshold stress below which no sliding occurs. Finally, there is no satisfactory explanation for the plasticity of nanometric polycrystals, which cannot be extrapolated from the laws valid for micro- and submicrometric ones.

     LINKS

Institute of Advanced Scientific Computation (ICCAEx)

NIST (National Institute of Standards and Technology, Gaithersburg, MD, USA)