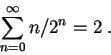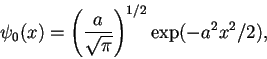FÍSICA CUÁNTICA. Convocatoria de Septiembre. 5/9/2002.
1. Una partícula de masa ![]() está ligada en un potencial
está ligada en un potencial
![]() ,
, ![]() . Encontrar el valor de
. Encontrar el valor de ![]() tal que la
probabilidad de encontrar a la partícula en la región
tal que la
probabilidad de encontrar a la partícula en la región ![]() sea
exactamente igual a 1/2.
sea
exactamente igual a 1/2.
(2.5 puntos)
2. En ![]() una partícula en un potencial
una partícula en un potencial
![]() está descrita por la siguiente función de onda:
está descrita por la siguiente función de onda:
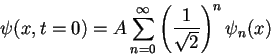
donde ![]() son los autoestados ortonormales del oscilador armónico con
energías
son los autoestados ortonormales del oscilador armónico con
energías
![]() .
.
(2.5 puntos)
3. Una partícula de masa ![]() está ligada en un potencial
tridimensional
está ligada en un potencial
tridimensional
(2.5 puntos)
4. Calcular el estado fundamental del calcio (Ca), ![]() ,
primero en presencia de la interacción residual y posteriormente
teniendo en cuenta la interacción espín-órbita. Realizar un
esquema del desdoblamiento del estado fundamental en presencia de un
campo magnético intenso.
,
primero en presencia de la interacción residual y posteriormente
teniendo en cuenta la interacción espín-órbita. Realizar un
esquema del desdoblamiento del estado fundamental en presencia de un
campo magnético intenso.
(2.5 puntos)
Ayuda: