FÍSICA CUÁNTICA. Examen final. 21/6/2002.

1.a Estimar:

1. Radio de Bohr (cm).
2. Magneón de Bohr (elíjase la unidad).
3. Constante de estructura fina.
4. Diferencia típica de energías en estructura fina.

1.b ¿Es posible observar la difracción de una pelota de tenis de masa 0.1 kg moviéndose a 0.5 m/s por una ventana de tamaño $1$ m $\times$ 1.5 m?

2.a Consideremos un experimento en el cuál se dirige un haz de electrones a una placa sólida que tiene dos rendijas (en lo que sigue rendijas A y B). Detrás de la placa se encuentra una pantalla equipada con un conjunto de detectores que permiten saber en que parte de la pantalla inciden los electrones.

Dibujar en una figura el número relativo de electrones que impactan como función de la posición sobre la pantalla ( y dar una pequeña explicación) en los siguientes supuestos:

1. Rendija A abierta y B cerrada.
2. Rendija A cerrada y B abierta.
3. Ambas rendijas abiertas.
4. Se acopla un dispositivo Stern-Gerlach delante de las doble rendija de tal manera que por la rendija A pasan solo electrones con tercera componente de espín $+\hbar/2$ y por B electrones con tercera componente de espín $-\hbar/2$.
5. Como en el caso anterior pero por la rendija A pasan solo electrones con tercera componente de espín $+\hbar/2$ y por B electrones con tercera componente de espín $+\hbar/2$.

2.b Una partícula de masa $m$ se mueve en un pozo de potencial de paredes impenetrables de anchura $l$ ($x\in (0,l)$). En $t=0$ la función de onda de la partícula es:

$$\psi(x,0)=\left\{\begin{array}{c c } \sqrt{\frac{30}{l^5}} ... ... ,\\ 0 & \mathrm{en\; el\; resto} \; . \end{array} \right.$$

Calcular $\psi(x,t)$.

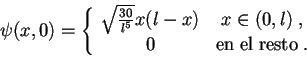
3.a Calcular el estado fundamental del argón (Ar), $Z=18$, primero en presencia de la interacción residual y posteriormente teniendo en cuenta la interacción espín-órbita.

3.b La componente $y$ del espín de un electrón es medida encontrándose $+\hbar/2$. Si medimos el espín en la dirección $(-1,0,0)$, ¿qué probabilidad se tiene de medir $-\hbar/2$?

4.a Un pozo cuadrado de pareces impenetrables de anchura $L$ ($x\in (0,L)$) se perturba con un término $V=\lambda \delta(x-L/2)$. Calcular, en primer orden en teoría de perturbaciones, las nuevas energías de los estados ligados.

4.b Una partícula de espín 1/2 tiene como hamiltoniano:

$$H=A S_x+ B S_x^2 \; ,$$

donde $A$ y $B$ son constantes. Calcular los niveles de energía y las autofunciones.

Nota $S_x=\hbar/2\; \sigma_x$, donde $\sigma_x$ es la primera matriz de Pauli.