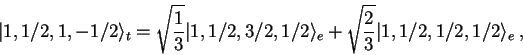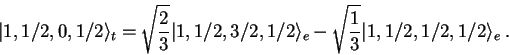FÍSICA CUÁNTICA. Segundo examen parcial. 31/5/2002.

1. Los quarks son partículas de espín 1/2. Tres quarks se enlazan para formar un barión (como por ejemplo los protones o los neutrones), mientras que dos quarks (más precisamente un quark y un antiquark) se enlazan para formar un mesón. Si los quarks están en el estado fundamental (por lo tanto su momento angular orbital es cero):

1. ¿Qué espines son posibles para los bariones?
2. ¿Y para los mesones?

(1.5 puntos)

2. El electrón de un átomo de hidrógeno tiene la siguiente función de onda:

$$R_{21} \left[\sqrt{\frac{1}{3}} Y_1^0 \left( \begin{array}{... ...t( \begin{array}{c } 0 \\ 1 \end{array} \right) \right] \; .$$

• Si medimos $L^2$, ¿ qué valores y con qué probabilidades podremos obtenerlos?

• Idem para $L_z$.

• Idem para $S^2$.

• Idem para $S_z$.

• Si medimos simultaneamente la componente $z$ del espín y la distancia del electrón al origen, ¿cuál es la densidad de probabilidad de encontrar a la partícula con tercera componente de espín $+\hbar/2$ y a una distancia $r$ del origen?

Sea $\mathitbf{J}=\mathitbf{L}+\mathitbf{S}$.

• Si medimos $J^2$, ¿qué valores y con qué probabilidades podremos obtenerlos?

• Idem para $J_z$.

  Ayuda: En las dos preguntas precedentes es muy útil consultar la ayuda al final del examen.

(2.5 puntos)

3. Calcular el estado fundamental del germanio (Ge), $Z=32$, primero en presencia de la interacción residual y posteriormente teniendo en cuenta la interacción espín-órbita.

(1.5 puntos)

4. Usando una familia de funciones prueba gaussianas, encontrar una cota superior a la energía del estado fundamental de:

$$H=-\frac{\hbar^2}{2 m} \frac{d^2}{dx^2} -\alpha\; \delta(x), \; \alpha>0 \; .$$

(2 puntos)

5. Un electrón del átomo de hidrógeno se encuentra en el estado $n=3$, $l=0$ y $m=0$ ( $\vert 3 0 0 \rangle$) y decae al estado fundamental ( $\vert 1 0 0 \rangle$) mediante una serie de transiciones dipolares eléctricas.

• Representar las posibles rutas por las cuales el estado de partida $\vert 3 0 0 \rangle$ puede llegar al fundamental (por emisión espontánea).

• Si tenemos una ``botella'' llena de átomos de hidrógeno en el estado $\vert 3 0 0 \rangle$, ¿qué fracción de ellos decaerán en cada una de las posibles rutas?

• ¿Cuál es la vida media (en segundos) del estado $\vert 3 0 0 \rangle$?

  Ayuda: Para el cálculo de la vida media solo hay que mirar la primera transición desde $\vert 3 0 0 \rangle$. Una vez que el estado ha ``saltado'' ya no es el $\vert 3 0 0 \rangle$!! Cuando hay más de una ruta abierta se suman las razones de transición y la vida media es el inverso de la citada suma.

(2.5 puntos)

Datos y ayuda.

Algunas funciones de onda del átomo de hidrógeno:

$$\psi_{100}=\frac{1}{\sqrt{\pi}} \frac{1}{a_0^{3/2}} e^{-r/a_0} \; .$$

$$\psi_{200}= \frac{1}{4 \sqrt{2 \pi}} \frac{1}{a_0^{3/2}} \left(2- \frac{r}{a_0} \right) e^{-r/( 2 a_0)} \; .$$

$$\psi_{210}= \frac{1}{4 \sqrt{2 \pi}} \frac{1}{a_0^{3/2}} \left(\frac{r}{a_0} \right) e^{-r/( 2 a_0)} \cos \theta \; .$$

$$\psi_{21\pm 1}= \frac{1}{8 \sqrt{\pi}} \frac{1}{a_0^{3/2}} \... ...{a_0} \right) e^{-r/( 2 a_0)} \sin \theta e^{\pm i \phi} \; .$$

$$\psi_{300}= \frac{1}{81 \sqrt{3 \pi}} \frac{1}{a_0^{3/2}} \l... ...rac{r}{a_0} +2 \frac{r^2}{a_0^2} \right) e^{-r/( 3 a_0)} \; .$$

La razón de transición (probabilidad por unidad de tiempo) espontánea entre los estados inicial ($\Phi_i$) y final ($\Phi_f$) es:

$$R_{i\to f}=\frac{ \omega^3 e^2 \vert( \Phi_f, \mathitbf{r} \Phi_i ) \vert^2}{ 3 \pi \epsilon_0 \hbar c^3} \;.$$

donde $\hbar \omega=E_i-E_f$, siendo $E_i$ y $E_f$ las energías de los estados inicial y final (respectivamente).

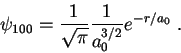
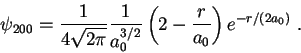
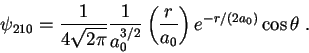
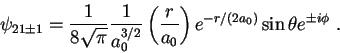
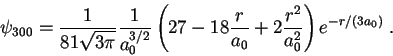
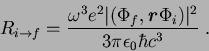
La siguiente integral es útil:

$$\int_0^\infty ds\; s^4 (27-18 s +2 s^2) e^{-5 s /6}=\frac{5^6}{2^8 3^9} \; .$$

Si $\vert L,S,J,M_J\rangle_e$ denota un elemento de la base estándar y $\vert L,S,M_L,M_S\rangle_t$ denota un elemento de la base tensorial, donde $\mathitbf{J}=\mathitbf{L}+\mathitbf{S}$, entonces:

$$\vert 1,1/2,1,-1/2\rangle_t= \sqrt{\frac{1}{3}} \vert 1,1/2,... ...angle_e+ \sqrt{\frac{2}{3}} \vert 1,1/2,1/2,1/2\rangle_e \; ,$$

$$\vert 1,1/2,0,1/2\rangle_t=\sqrt{\frac{2}{3}} \vert 1,1/2,3/... ...angle_e -\sqrt{\frac{1}{3}} \vert 1,1/2,1/2,1/2\rangle_e \; .$$