FÍSICA CUÁNTICA. Primer examen parcial. 11/2/2003.

1. La sección eficaz total de interacción del Hierro ${}^{56}_{26}\mathrm{Fe}$ con neutrones de energía cinética $K=20  \mathrm{GeV}$ es $\sigma=1.120\times 10^{-24}  \mathrm{cm}^2$. La densidad del Hierro es $\rho=7.27  \mathrm{g}/\mathrm{cm}^3$. Calcular el recorrido libre medio y el tiempo medio entre colisiones. (2 puntos)

2. Demostrar que, en una dimensión, se pueden elegir reales las funciones de onda de los estados ligados. (2 puntos)

3. Un resultado fundamental de la óptica física es que ningún instrumento óptico puede resolver los detalles estructurales de un objeto que sea más pequeño que la longitud de onda de la luz con que se está observando. A la longitud de onda de de Broglie se le aplica el mismo tipo de análisis. Si se desea estudiar un virus de $200 \AA$ de diámetro resulta imposible usar microscopios ópticos ( $\lambda \sim 5000 \AA$), pero si puede hacerse usando un microscopio electrónico. Calcular el voltaje con el que deben de acelerarse los electrones para que su longitud de onda de de Broglie sea 1000 veces más pequeña que el virus de modo que la imagen resultante sea realmente buena. (2 puntos)

4. Sea el siguiente potencial:

$$V(x)=\left\{ \begin{array}{l l} \infty & \mathrm{si}\;\; x\le0\;, \\ k x & \mathrm{si}\;\; x>0 \;, \end{array} \right.$$

donde $k$ es una constante positiva.

• Estimar la energía del estado fundamental mediante el principio de incertidumbre.

• Cuantizar el potencial usando las reglas de cuantización de Wilson-Sommerfeld.

• Encontrar las autofunciones (sin normalizar) y autovalores resolviendo de manera exacta la ecuación de Schrödinger. Ayuda: Expresar los niveles de energía en términos de los ceros de la función de Airy.

• Comparar los resultados obtenidos en los tres puntos anteriores.

• Calcular de manera clásica la probabilidad de que la particula se encuentre en el intervalo $(x,x+dx)$.

• ¿En qué condiciones la probabilidad calculada mediante Mecánica Cuántica estará convenientemente aproximada por la probabilidad clásica claculada anteriormente?

• Citar algún sistema físico que está descrito por el potencial $V(x)$.

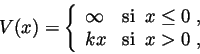
(4 puntos)

Ayuda.

La ecuación diferencial de Airy

$$u^{\prime \prime}(x) -x u(x) =0 \; ,$$

tiene como solución general

$$u(x)= c_1\mathrm{Ai}(x) +c_2 \mathrm{Bi}(x) \; ,$$

donde $c_1$ y $c_2$ son constantes de integración. Las funciones de Airy $\mathrm{Ai}(x)$ y $\mathrm{Bi}(x)$ tienen el siguiente comportamiento asintótico:

$$\mathrm{Ai}(x) \sim \frac{1}{4 \pi} \frac{1}{x^{1/4}} \exp\left[-\frac{2}{3} x^{2/3} \right]\; ,$$

$$\mathrm{Bi}(x) \sim \frac{1}{4 \pi} \frac{1}{x^{1/4}} \exp\left[+\frac{2}{3} x^{2/3} \right] \; ,$$

cuando $x\to \infty$.

Sean $a_s$ y $b_s$ los ceros de las funciones de Airy $\mathrm{Ai}(x)$ y $\mathrm{Bi}(x)$ respectivamente. En la siguiente tabla se pueden encontrar los cinco primeros ceros.

$s$	$a_s$	$b_s$
1	-2.33810	-1.17371
2	-4.08794	-3.27109
3	-5.52055	-4.83073
4	-6.78670	-6.16985
5	-7.94413	-7.37676