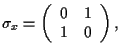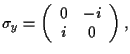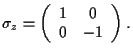Next: About this document ...
FÍSICA CUÁNTICA. Curso 1999/2000.
Examen Final. Convocatoria de Septiembre. 6/9/2000.
El examen consta de cuatro problemas (cada uno con dos subapartados)
en dos hojas.
Problema 1.
- El Sol tiene una masa
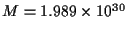 kg y un radio
kg y un radio
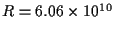 cm y emite aproximadamente como un cuerpo
negro a 5700 K. ¿Qué energía es emitida cada año en forma de
radiación? ¿Qué fracción de la masa solar representa esta
energía?
cm y emite aproximadamente como un cuerpo
negro a 5700 K. ¿Qué energía es emitida cada año en forma de
radiación? ¿Qué fracción de la masa solar representa esta
energía?
(1.25 puntos)
- La sección eficaz total de neutrinos con nucleones es de
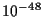 m
m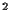 /nucleón. Estimar el recorrido libre medio de un
neutrino en el centro del Sol donde la densidad es de
/nucleón. Estimar el recorrido libre medio de un
neutrino en el centro del Sol donde la densidad es de
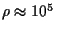 kg/m
kg/m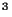 .
.
(1.25 puntos)
Problema 2.
Problema 3.
Problema 4.
- Sea el siguiente
potencial
donde 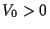 . 1) Calcular la ecuación trascendente que satisface la
energía de los estados ligados, para
. 1) Calcular la ecuación trascendente que satisface la
energía de los estados ligados, para 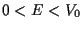 . 2) Sin realizar
ningún cálculo adicional, dibujar cualitativamente la función de
onda del estado fundamental.
. 2) Sin realizar
ningún cálculo adicional, dibujar cualitativamente la función de
onda del estado fundamental.
(1.25 puntos).
- Se prepara un estado con proyección de espín
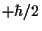 según la dirección del eje
según la dirección del eje 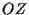 .
1) ¿ Cuál es el valor esperado del operador
.
1) ¿ Cuál es el valor esperado del operador 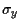 en este estado?
2) Si posteriormente medimos el espín en la dirección (0,1,1),
¿ Cuáles son los posibles resultados de la medida y con qué
probabilidades?
en este estado?
2) Si posteriormente medimos el espín en la dirección (0,1,1),
¿ Cuáles son los posibles resultados de la medida y con qué
probabilidades?
(1.25 puntos).
Ayuda:
- Constantes:
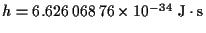 .
.
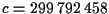 m/s.
m/s.
La carga del electron:
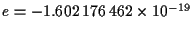 C.
C.
La constante de Stefan-Boltzmann:
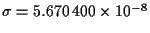 W/(m
W/(m K
K ) .
) .
La masa del protón:
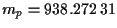 MeV/c
MeV/c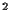 .
.
La masa del electrón:
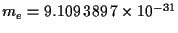 kg .
kg .
- El operador de espín para partículas de espín
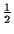 es
es
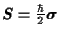 , donde
, donde
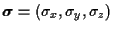 son las matrices de
Pauli dadas por:
son las matrices de
Pauli dadas por:
- La función de onda del estado fundamental de un átomo de
hidrógeno es
donde
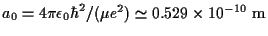 es el radio de Bohr. La energía del estado
fundamental está dada por:
es el radio de Bohr. La energía del estado
fundamental está dada por:



Next: About this document ...
Juan J. Ruiz-Lorenzo
2000-09-07
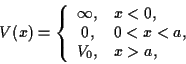
![]() .
.
![]() m/s.
m/s.
![]() C.
C.
![]() W/(m
W/(m![]() K
K![]() ) .
) .
![]() MeV/c
MeV/c![]() .
.
![]() kg .
kg .