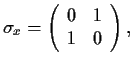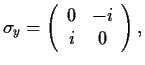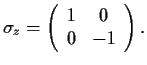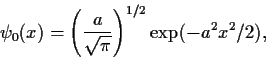FÍSICA CUÁNTICA. Curso 1999/2000.
Segundo Parcial. 19/5/2000.
El examen consta de cinco problemas en dos hojas.
1. Sea ![]() el operador momento angular de un
sistema. Sea
el operador momento angular de un
sistema. Sea ![]() un autoestado de
un autoestado de ![]() . Calcular
. Calcular
![]() y
y
![]() . Ayuda: Usar
las reglas de conmutación del momento angular. (2 puntos).
. Ayuda: Usar
las reglas de conmutación del momento angular. (2 puntos).
2. Se prepara un estado con proyección de espín
![]() según el eje
según el eje ![]() . ¿Cuál será la probabilidad de
que al medir, sobre el estado anterior,
la proyección del espín según el eje
. ¿Cuál será la probabilidad de
que al medir, sobre el estado anterior,
la proyección del espín según el eje ![]() se
obtenga
se
obtenga ![]() ? (2 puntos).
? (2 puntos).
3.a Calcular
![]() , donde
, donde ![]() es
la función de onda del
estado fundamental de un oscilador armónico con potencial
es
la función de onda del
estado fundamental de un oscilador armónico con potencial
![]() .
. ![]() es el operador momento lineal. (1 punto).
es el operador momento lineal. (1 punto).
3.b Calcular, en primer orden en teoría de perturbaciones,
la energía del estado fundamental de un oscilador armónico (con
potencial
![]() )
sometido a una perturbación
)
sometido a una perturbación ![]() . (1 punto).
. (1 punto).
4. Calcular las ecuaciones trascendentes que satisface la
energía de los estados ligados, para ![]() , en el siguiente
potencial
, en el siguiente
potencial
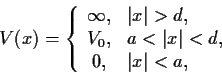
Ayuda: Resuélvase primero la ecuación de Schrödinger para las funciones pares y luego para las impares. (2 puntos).
5. En el instante ![]() un átomo de hidrógeno
se encuentra en el siguiente
estado (ignoraremos en este problema el espín del electrón):
un átomo de hidrógeno
se encuentra en el siguiente
estado (ignoraremos en este problema el espín del electrón):
Ayuda: