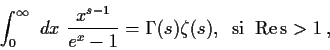FÍSICA CUÁNTICA. Curso 1999/2000.
Primer Parcial. 3/3/2000.
El examen consta de seis problemas en dos hojas.
1. En el Universo existe un fondo de radiación
electromagnética isótropa de espectro análogo al del cuerpo
negro, para una temperatura de ![]() K. Determínese el
número de fotones por cm
K. Determínese el
número de fotones por cm![]() y su energía media (en eV).
(1.5 puntos)
y su energía media (en eV).
(1.5 puntos)
2. Calcular, partiendo de los postulados de de Broglie, la velocidad de fase y de grupo para un neutrino electrónico (partícula de masa nula). Discútase el resultado. (1 punto)
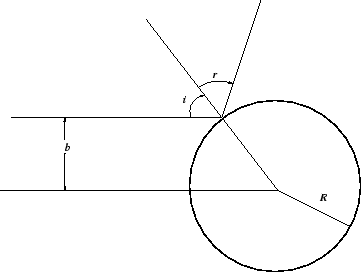
3. Calcúlese la sección eficaz diferencial (
![]() ) y total (
) y total (![]() ) en la dispersión elástica de
particulas puntuales por una esfera de masa infinita y radio
) en la dispersión elástica de
particulas puntuales por una esfera de masa infinita y radio ![]() . En
la figura,
. En
la figura, ![]() es el parámetro de impacto e
es el parámetro de impacto e ![]() y
y ![]() son los
ángulos de incidencia y de reflexión. Ayuda. a) ¿ Qué relación
deben de verificar los ángulos de incidencia,
son los
ángulos de incidencia y de reflexión. Ayuda. a) ¿ Qué relación
deben de verificar los ángulos de incidencia, ![]() , y de reflexión,
, y de reflexión,
![]() ? b)
? b)
![]() , donde
, donde ![]() es el
ángulo que forman el momento incidente y el momento dispersado. (2 puntos)
es el
ángulo que forman el momento incidente y el momento dispersado. (2 puntos)
4. Una pelota de masa ![]() bota de forma perfectamente
elástica, sobre una superficie horizontal, moviéndose siempre
según el eje
bota de forma perfectamente
elástica, sobre una superficie horizontal, moviéndose siempre
según el eje ![]() . Determínense los niveles energéticos por
medio de las reglas de cuantización de Wilson-Sommerfeld. (1.5 puntos)
. Determínense los niveles energéticos por
medio de las reglas de cuantización de Wilson-Sommerfeld. (1.5 puntos)
5. 1) Usando de nuevo las reglas de cuantización de
Wilson-Sommerfeld calcular los niveles energéticos del potencial
armónico tridimensional
![]() , donde
, donde ![]() es una constante y
es una constante y
![]() .
2) Usando argumentos basados en el principio de indeterminación
estimar la energía mínima del sistema. Comparar los resultados
obtenidos en los apartados 1) y 2). (2 puntos)
.
2) Usando argumentos basados en el principio de indeterminación
estimar la energía mínima del sistema. Comparar los resultados
obtenidos en los apartados 1) y 2). (2 puntos)
6. El ![]() es un mesón inestable neutro. Su principal modo de
desintegración da como resultado dos piones que por conservación
de la carga han de ser ambos neutros o cargados. Consideremos en lo
que sigue una desintegración en dos piones cargados. La masa del
pión cargado es de 139.6 MeV/
es un mesón inestable neutro. Su principal modo de
desintegración da como resultado dos piones que por conservación
de la carga han de ser ambos neutros o cargados. Consideremos en lo
que sigue una desintegración en dos piones cargados. La masa del
pión cargado es de 139.6 MeV/![]() . Se han medido los momentos (en
GeV/c) de los dos piones resultantes, obteniendose en el sistema de
laboratorio (datos reales obtenidos en el CERN):
. Se han medido los momentos (en
GeV/c) de los dos piones resultantes, obteniendose en el sistema de
laboratorio (datos reales obtenidos en el CERN):
![]() y
y
![]() . Calcular a) la
masa de
. Calcular a) la
masa de ![]() (en MeV/
(en MeV/![]() ), b) el módulo del momento de
), b) el módulo del momento de ![]() en
el sistema de laboratorio (en GeV/c) y c) su longitud de onda de de
Broglie en el sistema laboratorio (en m). (2 puntos)
en
el sistema de laboratorio (en GeV/c) y c) su longitud de onda de de
Broglie en el sistema laboratorio (en m). (2 puntos)
Ayuda:
La densidad de energía de un cuerpo negro es:
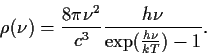
Constantes:
![]() .
.
![]() m/s.
m/s.
![]() C.
C.
![]() J/K.
J/K.
Integral: